Technical 03.09.2019, 16:37

The Arms Index aka TRIN

1. Introduction
2. Methodology
2.1 Analysis
2.2 Applications
3. Signal Analysis
4. Results
5. Criticism
6. Conclusion

1. Introduction

The index was created by Richard Arms in 1967 when he was working at a tiny retail broker called EF Hutton. He was looking at very common figures available on his terminal of the current stock market the number & volume of advancing and declining shares.

Richard had the idea to look at the ratios of the advancing and declining stocks numbers and volumes and one day decided to simply look at the ratio of the two ratios.

The Arms index is therefore a ratio of the number of stocks ratio and the volume ratio of stocks advancing and declining at any given moment. He showed this to a colleague, Newton Zinder, at the New York office, who gave it to Alan Abelson at Barron's, who was very keen on publishing. Soon after publishing it at Barron's it was referred to many traders and even started displaying at the NYSE Big Board under the code TRIN which it was most commonly referred to, the TRaders INdex [13].

"I came up with this stupidly simple indicator that combined the volume with the advancing and declining stocks. I was the first guy to think of it, but if i hadn't, someone else would have. The very simplicity is what makes it so effective." (Richard Arms) [13]

Richard went on to develop many other indicators involving the volume of shares. He introduced a style of plotting the share price movement like the candlestick method but where the width of each rectangle corresponded to the stocks volume trading on that day. It is called Equivolume, making it easier to spot low volume days or big excessive volume days just simply by a charting technique. He is a strong believer on the importance of the share volume as much as that in an 1991 interview with the Stock & Commodities magazine he was quoted as saying

"If the market were a wristwatch, it would be divided into shares, not hours." (Richard Arms) [14]

Richard Arms later on won the prestigious 1995 Market Technicians Award and has written a number of books on this subject. He is admired by many practicioners and regarded as one of the most famous market technicians of our time until he passed away recently (2017?).

NYSE Big Board showing the TRIN displayed (middle right)

2. Methodology

So how is it calculated? It consists of two ratios. The first ratio is the ratio of advancing to declining stocks.

Ratio 1 = Count of Advancing Stocks / Count of Declining Stocks

The second ratio is the ratio between the stock volume of advancing and declingin stocks.

Ratio 2 = Stock Volume of Advancing Stocks / Stock Volume of Declining Stocks.

The TRIN is the number you get when you divide Ratio 1 by Ratio 2.

Trin = Ratio 1/Ratio 2

Another way to write it would be like this

TRIN = (A/D) / (AV/DV) = ( A * DV ) / ( D * AV ) [Eq.0]

where

A = number of advancing shares

D = number of declining shares

DV = sum over all declining volume

AV = sum over all advancing volume

and where we sum over all shares traded regardless of dollar-value and simply count the number of shares advancing or declining similar to the ADL.

2.1 Analysis

It is clear that if you have a day where the advancing volume (AV) is zero or the count of declining shares (D) is zero you are going to be dividing by zero which leads to a singularity or technically infinity.

You could write the function as such

f(x,y) = A / x*y

Illustrative sample chart of the TRIN function for stock counts from 0 to 100 and volume from 0 to 100,000.

So clearly this index is not good around the start of the trading day, because each day you start counting at zero. It also doesnt work in the above 2 cases where either AV or D is zero. So a day where you only have declining volume or a day where you only have advancing stocks. This could be more frequent than you think since you are not counting stocks which are not moving at all as either declining or advancing. Stocks which are not moving on the day, ie have the same trade price as the previous day will not get counted towards either A or D, or AV or DV likewise.

It is also clear that when you have a day when your advancing and declining stocks are of the same count and the advancing and declining volume are the same that you will end up with an indicator of 1.0 since both ratios will need to necessarily be 1, or the product of A*DV and the product of D*AV need to coincidentally be exactly the same.

TRIN = 1 = A*DV / D*AV

therefore the index is =1 if either of these cases occur.

D * AV = A * DV [Eq 1] or , A/D = 1 & AV/DV = 1

or the ratio of AV/DV is exactly the same as the ratio of A/D

AV / DV = A / D

What does Eq [0] mean for the market? If we have a very bullish market day with almost all stocks up then A/D is going to be very high, it is highly likely that the ratio is going to be similarly high AV/DV. If the two ratios are the same we have a TRIN =1. How are we going to get very low levels of TRIN << 1? We are going to get this when the ratio of AV/DV is much bigger than the ratio of A/D is. That means a very high advancing volume AV bigger than the declining volume DV yet a lower count of advancing stocks compared to declining stocks. So that means a bigger volume in fewer advancing stocks (TRIN<<1). Likewise the opposite case when TRIN is much bigger than 1 (TRIN >>1) happens when we have a bigger volume in fewer declining stocks (TRIN>>1).

Since the volume count is purely absolute there is no dollar value associated with this, we cannot say that if we are looking at tiny cap stocks getting all the volume. One thing to note here is that while the number of stocks is fixed there is a minimum & maximum ratio of A/D, but for AV/DV there is no such limit. The number of stocks are always integers on a finite range but the volume is a also always integers but on a theoretically infinite range. Lets say your number of stocks you are counting is max 100 shares for simplicity. You will have a minimum of 1/99=0.01 and max of 99/1=99 except for the obvious extreme cases of either one being 0. But for the volume you might have for example a case of 1/1,000,000,000 = 0.000000001 or 1,000,000,000/1 = 1,000,000,000. Leading to TRINs of 0.01/0.000000001= very big or 99/100,000,000= very tiny. Meaning that the AV/DV ratio is most likely dominating this indicator over the A/D ratio just purely by nature of numbers. This is why Richard Arms says that a TRIN>1 is bearish and a TRIN<1 is bullish.

Lets simplify Eq [1] by two transformations. We know the number of stocks is fixed, so the sum of all advancing, declining and unchanged stocks is a fixed number lets call it N.

We can write

N = A+D+ε

and further write A in terms of D as

A = N* - D

where we assume N*=N+ε is almost identical since ε is going to be small. Likewise we can simplify the volume to assume there is a constant volume of shares traded each day which is fixed. Then we can write similarly

M = AV + DV + ε

and also

AV = M* - DV.

Substituting this into Equation [1] we get

D × ( M* - DV ) = ( N* - D) × DV

which expands leading to

DV = M*/N* × D

or if we want to express it in terms of AV

D = N* - N*/M* × AV.

This simply means that the TRIN index is equal to 1 when the ratio of Declining Volume to Descending Stocks is the same as the ratio of total Volume to total number of stocks.

If we knew the total volume traded everyday and we already know the total number of stocks we know exactly when the TRIN will be 1.0, precisely when the Declining Volume has the same ratio to the Declining stocks count as the M*/N* ratio. Furthermore this means that there is a linear relationship between the Volume and the Count where the TRIN index is 1.0. We are going to draw this into a contour plot of Volume versus Stocks.

Using these substitions in Equation [1] we arrive at this

TRIN = ( N* / D - 1 ) × ( M* / AV - 1) [ Eq 3]

which is zero at D=N* and AV = M* which is simply the same as saying D=0 or A = 0. Trivial. It also has singularities at D=0 and AV=0. So at the very start of counting or measuring the traded volume, if either of them is still zero we are going to have a singularity.

In summary

D=0 or AV=0 TRIN ---> infinite (bottom and left of chart)
A=0 or DV=0 TRIN ---> zero (top and right of chart)

Contour plot of the TRIN, showing the area less than 1, greater than 1 and the line where T=1.

Lets expand Equation [3] we arrive at a mixed quadratic equation

TRIN = N* M* / (D AV) - N*/D - M*/AV + 1

or write this in terms of x=D and y=AV

TRIN(x,y) = N*M*/ (x y) - N*/x - M*/y + 1

If you remember the derivative of 1/x you will remember that the first derivative of 1/x is -x^-2. Meaning the slope of this curve decreases faster than the curve itself since its to the power 2. We have a gently sloping function out to the max values and infinity around either side being zero.

2.2 Applications

Lets start looking at applications. Arms considers anything above 1.25 to be oversold and values below 0.75 to be overbought.

Michael Sincere's book [13] suggests anything above 2.0 on the close to be a buy signal. Above 4.0 is a strong buy. If the TRIN drops below 0.5 on the close it is a sell signal and below 0.3 a strong sell.

Tim Ord (Secret Science of Price and Volume, Wiley, 2008) suggests above 3.0 is a market panic and above 5 or 6 we can have a peak.

Newton Zinder (from EF Hutton & Co) has determined that a consecutive 2 day reading greater equal 2.0 is bullish [14].

Robert Nurock (from WallStreetWeek TV) uses the TRIN in his Wall Street Week Index and considers a 10 day moving average reading above 1.2 to be bullish and a reading below 0.8 to be bearish.

Richard Arms considers a bullish signal when the 10 day moving average of the TRIN is below 0.8 and a bearish signal when the 10 day moving average of the TRIN is greater than 1.2. Other traders consider the lower bound to be 0.5 and the upper bound to be 2.0.

Alphier and Kuhn [15] look at levels greater than 2.56 over 21 years and found that it strongly suggests that these entry points are very likely going to be profitable. They bought at this trigger and held for 8 months unless there was another signal in that period. They were only in a position 54% of the time and produced 441% returns compared to a buy and hold strategy of 192% return. They note that the TRIN is a good measure of the market fear and a good indicator for market bargains.

Richard Arms considers values below 1.0 to be bullish and above 1.0 to be bearish. He writes that a level of 1.0 is a balance between advancing and declining stocks. But as we have derived above, a value of TRIN =1 may be achieved without A=D and AV=DV necessarily. This special case when A=D and AV=DV is simply the middle-point along a linear path in the space of count and volume of stocks. This is important to note since we are saying also that if the ratio's of the two is the same then you end up with dividing R (the Ratio) with R and R/R = 1. So it is not necessarily the value where you have the same number of advancing as declining stocks and the same volume of advancing as declining stocks. And is far from an equilibrium as we normally understand it. It is simply saying that there the number of advancing shares related to declining shares is identical to the amount of shares traded of advancing to declining shares. In that sense maybe the market is at 'parity' or 'equally distributed' between advancing and declining stocks, but it is far from a balance between advancing to declining stocks as Richard Arms suggests [16].

Colby [11] finds that levels greater than 1.444 and below 0.523 were bullish and statistically significant at the 99% confidence over a 1-year holding period. They explain that no only extremely high levels but also extremely low levels of the index are bullish entry signals. For shorter holding periods of 1 and 3 months readings of 0.523 or lower were also bullish but at 95% confidence. TRIN levels above 0.523 but below 1.444 had no significance [11]. Colby also looked the performance of a 10 day moving average and found that levels greater than 1.266 were very bullish over 1 year holding period and had a confidence level of 99.9%. He also used repeated buy signals to extend the holding period as above mentioned authors.

Richard Arms recommends levels for various moving averages on his website, they are

MA Overbought Oversold

4 day <0.75 >1.25

10 day <0.7 >1.20

21 day <0.85 >1.10

55day <0.9 > 1.05

[Note: Why does Dick choose the 21 and 55 day? He likes the Fibonacci numbers since they give him a naturally expanding time frame and also he admits in his course [18] Fibonacci adds a little bit of pzazz and mystique to this for his clients.]

In addition to the Index being bullish and bearish around 1.0 Arms suggests that for extreme readings above and below they are the indicating the opposite to what they are indicating in the vicinity. So somewhere there has to be a turning point between bullishness and bearishness and likewise. He suggests that levels much greater than 2.0 are signs of being oversold and levels much lower than 0.5 signal overbought situations.

Similar to Alphier and Kuhn [15] oder Colby [11] they find that being contrarian these points is profitable.

Now we want to determine when are points at which we should be bullish and bearish and have the biggest chance of making profitable trading decisions. Using the results we have derived above we are going to determine them in the following section.

3. Signal Analysis

What are good level to use? You can see from above there are various different methods and applications of this signal. Practicioners have empirically or through statistical calculations come up with levels which they found profitable. Their levels are applicable to their assumptions and the specific set of stocks that they have used to calculate. What are the significant thresholds in the real world? How do we determine them? How can we determine useful levels from various sets of stocks?

One normally looks at averages, moving averages and standard deviations away from the mean. Can we do this here? Standard deviations assume that the data is normally distributed, meaning that they fluctuate equally around the mean. Statistically we can test whether data is normally distributed, there are a number of tests developed to check for normality. However lets first look at a histogram of the distribution and compare this visually to a normal distribution of corresponding mean and standard deviation.

Distribution of NYSE TRIN data compared to a normal dsitrbution of the corresponding mean and standard deviation (left) and a QQ plot (right)

The average here is 1.10 and has a standard deviation of 0.47 yet you can see a mass of values occuring around 1.0 and largely below 1.0, while fewer are above 1.0 but they are more extreme. The distribution is not symmetric around the average is one thing to note. It also visually doesnt seem to fit into a normal distribution just by looking at it, it has much too narrow and peaks are too high. How do we statistically test for normality?

There are a number of tests to run on this data to see whether it passes normality. The results are as follows

Shapiro-Wilk : p < 2.2e-16
Kolmogorov-Smirnov : p < 8.162e-7
Jarque Bera : p < 2.2e-16

Since all of them are much smaller than the required level of 0.05 we can conclude that the data is not normally distributed. Another way to evaluate normality is to do a QQ plot which is shown above.

Again the data points don't lie within the 5% confidence interval around the ideal normal distribution.

What would be a way to make the data possibly look more normally distributed ? We have to realize that we are dealing with a data set that is bounded by 0 on the left ie.

TRIN ∊ [ 0, ∞]

whereas normally distributed data is ∊ [ -∞, ∞]. We could look to transform the data using the logarithm since this function maps the range [ 0, ∞] to [ -∞, ∞]. Lets do that and visually inspect the data now using the new mean 0.02 and standard deviation 0.42.

Distribution of the logarithm of the NYSE TRIN data compared to a normal distribution of the corresponding mean and standard deviation (red).

It still looks off quite a bit and if we do the same normality tests as above we dont get any different values than before, which is not a surprise.

We could investigate further to see if we can fit a different kind of distrubtion to the data, but a quick look through the common ones we couldnt find any similar distributions. But in any case what are we interested in? Similar to the standard deviation we are interested in what level of the TRIN we are going to have outliers, or where we have a high chance of probability that the level of the TRIN will revert. With the 1 and 2 times standard deviation we look at the common 68.2% and 95.4% of population. Here we also want to look at these percentages but we find its more useful to look at 85% and 95.4%. That means that we are looking at cases where we have a 85% or 95.4% chance of reversion to the mean giving us excellent odds at winning on either up or down days.

Subsequently we are always going to chart the following number of levels

TRIN (grey)
TRIN 5 day moving average ( Short Term Average) (blue)
TRIN 10 day moving average (Medium Term Average) (pink)
TRIN 100 day moving average (Long-Term average) (black)
TRIN4.6 — 4.6% probability (200 days) (green dotted)
TRIN15 — 15% probability (200 days) (green)
TRIN85 — 85% probability (200 days) (red)
TRIN95.4 — 95.4% probability (200 days) (red dotted)

We look at a moving probability because it makes sense to monitor it as time passes, the window of 200 is maybe too short but should be adjusted the more data is captured and will improve accuracy of the data. But at some point one will have to compromise between moment and long-term observations. Now lets get to the Results.

4. Results

Lets look at the official TRIN data for the NYSE. Looking at the chart you see the actual data (grey), a 5 day moving average (blue), a 10 day moving average (pink) and a 100-day moving average (black) together with the 4 probability levels in red and green. You also see the reference fixed lines at 0.5 and 2. Current values for the probabilities are

TRIN15%	TRIN85%	TRIN4.6%	TRIN95.4%
0.8	1.46	0.62	1.87

Compare this to the levels mentioned above of 1.444 and 0.523 at 99% confidence what Colby found. It seems almost similar except for the upper bound we would suggest to use 1.87. The approach we use is differnet to Colby's, where he measures the performance for 6-12months after a certain level is breached. We only look at the probability of the occurrence of such a signal and the deviation from the equilibrium (around the mean) and we expect that significant deviations from the mean will lead to reversals. We dont really need to look at the price performance subsequently to know if its going to be profitable or not. We are just going to leave this here as a conjecture, which still needs to be proven.

What else does this chart tell us? We can confirm what we saw from the data above that the equivalent levels of 15 and 85% and 0.046% and 95.4% are not symmetric around the mean. We also can confirm that the commonly mentioned levels of 0.5 and 2.0 fixed are good levels to use, but you are not going to catch all the entry points you wished for since you are probably looking at 99.9% chance of reversal, the mega-extreme cases so to speak. This is not going to give you enough good entry points and we prefer to look at a moving probability curve over a reasonably long time frame.

The asymmetry around the mean becomes even more apparent if we look at the TRIN for all our US underliers. Our levels become

TRIN15%	TRIN85%	TRIN4.6%	TRIN95.4%
0.8421	1.3914	0.7059	1.5663

So while these look similar on the low end of probabilities, they look completely different on the high end. You will need to monitor entirely different levels in this case.

Lets look at all stocks that we monitor globally, again the levels are asymmetric around the mean as expected and they are

TRIN15%	TRIN85%	TRIN4.6%	TRIN95.4%
0.7249	1.14641	0.6088	1.9031

We will get different triggers looking at different numbers of stocks, which seems obvious. But its important to note, since if you are trading the futures across regions, or say you dont want to trade the US market because thats where everyone is trading and looking at, you want to look at other regions, where you will have a bigger chance of reaping profits because simply the index is not calculated and published as widely as on the TRIN NYSE.

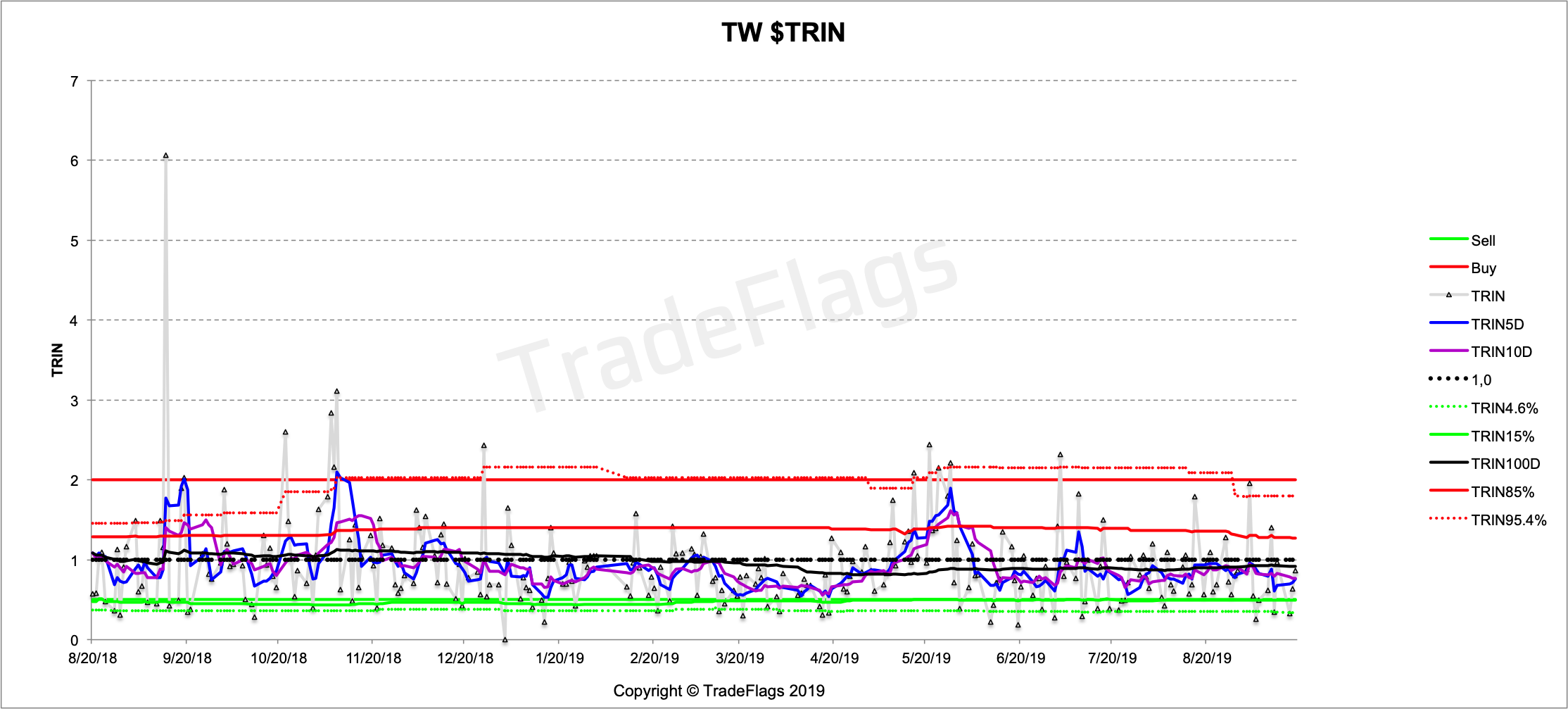
Interesting also is to look at regions or countries in particular. We investigate for this study Taiwan (TW), Hong Kong (HK), Germany (DE) and Australia (AX). And their charts are looking like this:

Time Series of TRIN for Hong Kong (HK), Taiwan (TW), Australia (AX) and Germany (DE).

5. Criticism

One critique of this index is the ratio of volumes we use. We can argue that this through the ratio of advancing and declining volume it is overestimating the impact of smaller value stocks, that is stock prices which are smaller, as compared to stocks with bigger stock prices. Assuming we had all stocks pretty much all similar order of magnitude of dollar value we would be satisfied with using just simply the volume to calculate a ratio of volumes. Yet when you have a big amount of stocks with very small prices compared to a few stocks with very large prices, you are going to overestimate the impact of these smaller stocks, since you will exagerate the impact a small notional of USD traded as compared to the impact of big $ notionals traded.

It would seem reasonable to assume that the volume increases roughly with decreasing $ price of the stock, but will drop off towards the very small illiquid names and drop off towards the really expensive names due to illiquidity. So there is somewhere a likely linear relationship between stock price and volume that may or may not breakdown. But why leave the possibility of this contamination in the Index? Why not remove it?

We assume that Richard back in the old days at his then cutting-edge terminal had only the Net Volumes available and not the $ Net Volumes. And we are pretty sure if he had had the $ Net Volumes available he would have definitely have preferred using the $ notional ratio instead of the volume ratio. On the other hand the ratio of advancing issues to declining issues is irrespective of $ notional as well. Should one weight this ratio as well and count stocks of higher dollar price more than stocks of smaller dollar value? This is probably an idea worth looking at and a point for further study. We suggest a ratio of dollar-weighted A/D and dollar weighted volume is probably a more accurate indicator since it wont be distorted by the dollar values of the stocks.

Whats a common distribution of stock prices on the US market. We can plot a histogram of stock prices and bucket them in $ buckets to see how it is distributed.

Distribution of Prices for the US (top left) and Global (bottom left) and closeups of US and Global (top right and bottom right)

You can see that by summing over the volume only one is equating the value of 1 stock purchase of tiny $ price the same way as 1 stock purchase of a 1000$ stock. The Arms Index is therefore not weighted according to the market cap of the stock which you might be forgiven to assume, but instead to the dollar-value of the stock. The smaller $-values of the stocks contaminate the volume traded on an otherwise equally weighted index. The case where all the stocks would have an equal weight would only be if all the stocks had more or less the same dollar-value, which is clearly not true (see figure), instead the $-value curve is steeply skewed towards small dollar values. You can explain this to the laymen in very simple terms as such:

Say you were a fruit and veggie trader and you had 'good' and 'rotten' produce, then the number of 'good' versus 'rotten' produce was indeed an interesting number (here A/D), but when it comes to the count of such 'good' and 'rotten' produce, if you had to fill a truck full of the rotten produce and you knew it was a 1000 pieces, you would want to know is it 1000 blueberries or 1000 pumpkins, since you won't necessarily fit a 1000 pumpkins into your truck.

Same applies here, what we are interested in is the $-volume of each stock and sum of the 'advancing' volume ('good' volume) and 'declining' volume ('rotten' volume).

Therefore we won't touch A/D as its normalized already, and every stock is treated equally, but we normalize the AV/DV ratio by the weight corresponding to the total net dollar-weight of all stocks. When we do this we get the following 'Normalized TRIN' and for the US stocks it looks like this

You can see the period around December 2018/ January 2019 is a lot more pronounced towards the SELL side than before and we think it clearly shows you it is working a lot better than non-normalized. Lets look further back into the past we get this

Here you can see the Feb 2018 selloff peak very very clearly as a very extreme level. So high that even the 5 day and 10 day average get pulled beyond a 97% probability level. We also see the peak in September 2018 which is also a significant date which kind of set the start off a broader selloff that peaked in December/January of 2018/2019.

6. Conclusion

We have analysed the TRIN Index by Richard Arms here. We have shown that there exists an infinite amount of possibilities for a TRIN level of 1.0 along combinations of advancing stocks and declining volumes. We have shown that this is not necessarily an equilibrium level where this occurs. We have gone through past empirical findings and statistically analysed the TRIN distribution. Subsequently we have derived values where the possibilities of reversals are maximized and found them to be in line with empirical findings yet more precisely defining a level of precise statistical chance. We have derived levels for the NYSE, the US stock market as a whole, the global stock market and specific markets such as Australia, Germany, Taiwan and Hong Kong. In all these regions we arrive at different levels to trade. Finally we have suggested some possible improvements over the standard TRIN index calculation.